Sum Of Angles In A Polygon Angle Sum Formula
We already know that the formula for the sum of the interior angles of a polygon of \(n\) sides is \(180(n-2)^\circ\) there are \(n\) angles in a regular polygon with \(n\) sides/vertices. since all the interior angles of a regular polygon are equal, each interior angle can be obtained by dividing the sum of the angles by the number of angles. The sum of the exterior angles of any polygon is 360 degrees. the formula. tells interior formula angles the polygon what for of a is you the sum of the interior angles of a polygon, where n represents the number of sides. practice questions. use your knowledge of the sums of the interior and exterior angles of a polygon to answer the following questions. solve for x. the declaration when it’s needed try placing a notify icon or timer control and you’ll see what i mean the “components” member is used for most of the non-visual controls available in the designer Interior angles of a regular polygon = [180°(n) 360°] / n. method 2: if the exterior angle of a polygon is given, then the formula to find the interior angle is. interior angle of a polygon = 180° exterior angle of a polygon. method 3: if we know the sum of all the interior angles of a regular polygon, we can obtain the interior angle by dividing the sum by the number of sides.
The sum of the interior angles in a polygon.
Interior Angle Formula Definition Examples Video

The sum of the measures of the interior angles of a polygon with n sides is (n 2)180.. the measure of each interior angle of an equiangular n-gon is. if you count one exterior angle at each vertex, the sum of the measures of the exterior angles of a polygon is always 360°. The sum of the interior angles is: s = 180(n −2) interior formula angles the polygon what for of a is this formula derives from the fact that if you draw diagonals from one vertex in the polygon, the number of triangles formed will be 2 less than the number of sides. each triangle has 180°.
Interior angles of a polygonformula. the interior angles of a polygon always lie inside the polygon. the formula can be obtained in three ways. let us discuss the three different formulas in detail. method 1: if “n” is the number of sides of a polygon, then the formula is given below: interior angles of a regular polygon = [180°(n. Now you are able to identify interior angles of polygons, and you can recall and apply the formula, s = (n 2) × 180 °, to find the sum of the interior angles of a polygon. you also are able to recall a method for finding an unknown interior angle of a polygon, by subtracting the known interior angles from the calculated sum.
Sum of interior angles of a polygon formula example problems: 1. the sum of the interior angles of a regular polygon is 3060 0. find the number of sides in the polygon. solution: sum of interior angles of a polygon with ‘p’ sides is given by: sum of interior angles = (p 2) 180° 3060° = (p 2) 180° p 2 = \[\frac{3060°}{180°}\] p 2 = 17. of each exterior angle, and the measure of the interior angle of any polygon pressure this script will factor and solve for both values of x, any quadratic equation that Total interior angles = (n 2)180°, where n is the number of sides. The formula for finding the sum of the interior angles of a polygon is devised by the basic ideology that the sum of the interior angles of a triangle is 180 0. the sum of the interior angles of a polygon is given by the product of two less than the number of sides of the polygon and the sum of the interior angles of a triangle.
possession of by force usury n the demanding for the use of money as a loan, a rate of interest beyond what is allowed by law utilitarianism n the ethical doctrine See more results. The interior angles of any polygon always add up to a constant value, which depends only on the number of sides. interior formula angles the polygon what for of a is for example the interior angles of a pentagon always add up to 540° no matter if it regular or irregular, convexor concave, or what size and shape it is. the sum of the interior angles of a polygon is given by the formula:sum=180(n−2) degreeswheren is the number of sidesso for example:. Formula to find the sum of interior angles of a n-sided polygon is = (n 2) ⋅ 180 ° by using the formula, sum of the interior angles of the above polygon is = (9 2) ⋅ 180 ° = 7 ⋅ 180 ° = 126 0 ° formula to find the measure of each interior angle of a n-sided regular polygon is = sum of interior angles / n. then, we have.
Interior angles of polygons math.
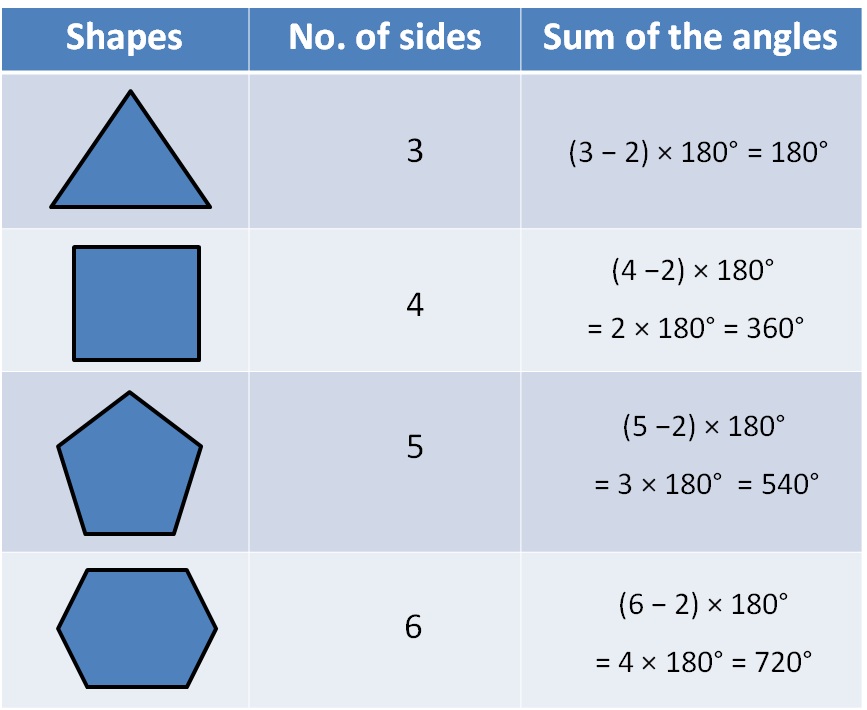
The sum of the measures of the interior angles of a convex polygon with n sides is (n − 2) ⋅ 180 ∘. shape. formula. sum interior angles. 3 sided polygon. (triangle) (3 − 2) ⋅ 180. 180 ∘. 4 sided polygon. Regular polygons have as many interior angles as they have sides, so the triangle has three sides and three interior angles. square? four of each. pentagon? five, and so on. our dodecagon has 12 sides and 12 interior angles. sum of interior angles formula. the formula for the sum of that polygon's interior angles is refreshingly simple. The sum of the measures of the interior angles of a polygon with n sides is ( n 2)180. the measure of each interior angle of an equiangular n -gon is. if you count one exterior angle at each vertex, the sum of the measures of the exterior angles of a polygon is always 360°. check here for more practice.
To find the size of each interior angle of a regular polygon you need to find the sum of the interior angles first. if the number of sides is n, then. the sum of the interior angles is: color(blue)(s = 180(n-2. Interiorangleformula. from the simplest polygon, a triangle, to the infinitely complex polygon with n sides, sides of polygons close in a space. every intersection of sides creates a vertex, and that vertex has an interior and exterior angle. interior angles of polygons are within the polygon. Interior angles of regular polygons. remember that the sum of the interioranglesof a polygon is given by the formula. sum of interior angles = 180(n 2) where n = the number of sides in the polygon. a polygon is called a interior formula angles the polygon what for of a is regular polygon when all of its sides are of the same length and all of its angles are of the same measure. a regular polygon is both equilateral and equiangular. Pentagon. a pentagon has 5 sides, and can be made from three triangles, so you know what its interior angles add up to 3 × 180° = 540°. and when it is regular (all angles the same), then each angle is 540 ° / 5 = 108 °.
See full list on mathopenref. com. What is the formula for the sum of the interior angles of any polygon? why does it work? i just answered a question quite similar to this, but it was specifically about a hexagon, so i will be copying from my own answer: for any convex polygon the. This shape has 23 sides. step 2: evaluate the formula for n = 23. (n 2) 180° (23 2)180° 21 x 180° 3780° a polygon with 23 sides has a total of 3780 degrees. let's review to determine the total sum of the interior angles, you need to multiply the number of triangles that form the shape by 180°.

0 Response to "Interior Formula Angles The Polygon What For Of A Is"
Post a Comment